An entire industry has been built around the idea that Byron's daughter Ada Lovelace was a great mathematician and the world's first computer programmer. Both of these claims are based on verbose notes she made to her 1843 translation of an 1842 paper by Menabrea about Charles… pic.twitter.com/gSQW8eCY3g
— Gavan Tredoux (@gtredoux) October 22, 2024
An entire industry has been built around the idea that Byron's daughter Ada Lovelace was a great mathematician and the world's first computer programmer. Both of these claims are based on verbose notes she made to her 1843 translation of an 1842 paper by Menabrea about Charles Babbage's Analytical Engine, an analog cogwheel-and-pinion computer which existed mostly on paper only (see https://drive.google.com/file/d/16qxC5R3Nr8FhET006LNe0sFeU8QDZ-29/view?usp=sharing). Both claims are entirely false. Here I will address the issue of her mathematical abilities.
Dorothy Stein was the first to point out in 1985, based on reading Ada's correspondence with Mary Somerville and Augustus de Morgan that Byron's daughter appeared to have very weak mathematical abilities. She could not do simple algebra. It is easy to verify this, without resorting to her manuscripts, by actually reading her published 1843 notes to Menabrea, a step few if any people ever seem to have taken the trouble to do. After all they're very long and use a lot of symbols. Here I will address only those on the Bernoulli numbers and their supposed calculation (see Note G in the paper). But this is just the basking seal on top of the iceberg, so to speak: the whole paper is riddled with bellowing nonsense, of which more later.
Babbage had been planning to use the Bernoulli numbers (from the power series expansion for a common expression involving e^x) as an example for his engine since 1835, as he wrote to Nathaniel Bowditch that year. In his memoirs he admitted (long after the fact) that he had worked out the details of this for Ada, "to save her the trouble". We can now see how this worked.
What Babbage had given Ada was just a brief sketch, which she expanded, in her prolix style, to match her understanding of the material. The crux was that Babbage wanted to accumulate calculations of Bernoulli numbers, as you would when constructing a table, something like his earlier Difference Engine, which used cumulated finite differences to do calculations of numerical results for tables. With some simple manipulations of the power series for e^x, see attached, an expression for the next odd indexed Bernoulli number can be obtained from the preceding ones. (Similar reasoning applies to the even indexed ones.) That follows from this relationship, a linear dependency, which we will write as equation (8), see attached
A_0 + A_1B_1 + A_3B_3 + .... + A_(2n-1)*B_(2n-1) + B_(2n+1) = 0. (8)
where the B_i are the odd Bernoulli numbers, and the A_i are coefficients which, as Ada failed to understand, actually depend on n too and are not constants. To get an expression for B_(2n+1), use your arithmetic superpowers to deduce (8*)
B_(2n+1) = -A_0 - A_1B_1 - A_3B_3 - .... - A_(2n-1)*B_(2n-1)
It is a step that sorely puzzled Ada though. She felt compelled to come up with an explanation anyway. She appears to have landed the world's smallest grappling hook on the phrase "linear dependence", probably used by Babbage in conversation with her. Scanning the equations she convinced herself that this "linear dependence" must apply to the index n, which she triumphantly concluded was dependent on its distance d from 0. So she wrote down some useless tautologies about that. Since you cannot do anything with them, she left them out there and simply moved on to point out that terms not listed in (8) must be zero (!) and wrote down a tautology involving multiplication and division by one, in which she gets the (irrelevant) indexes wrong for good measure (see attached for this extraordinary gibberish). This concludes her explanation. It has stood unexamined since 1843 by people who solemnly pronounce on the evidence it shows for her advanced abilities (!)
Why didn't Babbage notice this nonsense and correct her, supplying the necessary arithmetic superpowers? Correspondence shows that once she started writing her "notes", at his suggestion, she would accept no correction, So one assumes he simply stopped reading it, or at least commenting on it. Don't dare presume to alter what I, a daughter of Byron, write! So much for that.
Not realizing that the A_i terms depend on n too had further implications. You need to recalculate them when accumulating Bernoulli numbers iteratively, a step that eluded her and which undoes much of the sort of computational "saving" that Babbage was claiming. Indeed the execution trace (for the paper only contains such traces, not programs as such) doesn't work. Indeed none of the traces given in the paper for terms involving n could ever have been produced by Babbage's machine. More on that later. And on Ada's information that one can calculate a divergent (or indeed oscillating) infinite series on a computer, term by term. And why Babbage chose to use Menabrea and less successfully, Ada, in the first place. Not to mention what Babbage meant by The Enchantress of Number (hint: it was not Ada). Do not adjust your set.





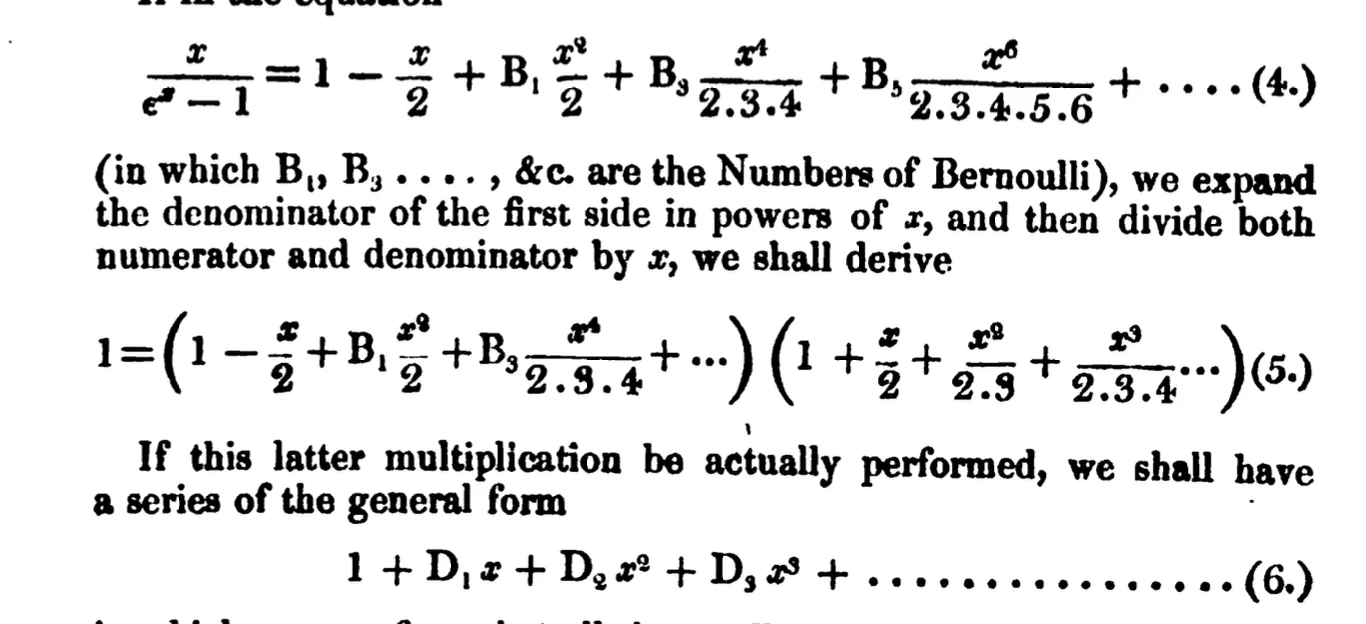

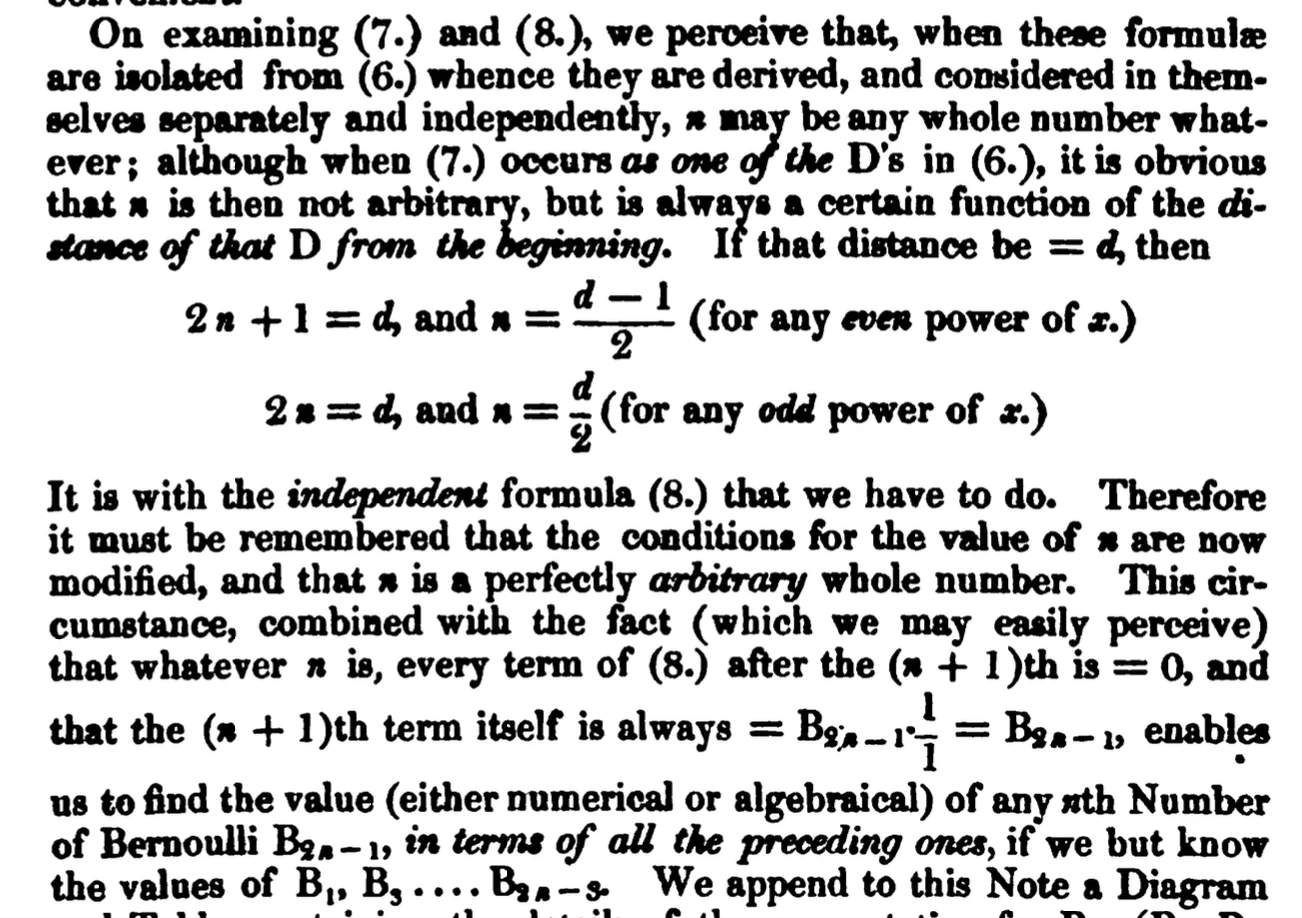


Jump in the discussion.
No email address required.
@GhoulishWails stand with Israel
Jump in the discussion.
No email address required.
most iq researchers arent wrong but they are annoying and therefore r-slurred
Jump in the discussion.
No email address required.
More options
Context
more gurl math
math  1842 wasn't 200 years ago!!!!!
1842 wasn't 200 years ago!!!!!
Jump in the discussion.
No email address required.
More options
Context
More options
Context